DIPOLAIRES (MOMENTS)

DIPOLAIRES (MOMENTS)

Lorsque, dans une molécule ou dans une liaison chimique, les barycentres des charges électriques positives et négatives ne coïncident pas, la juxtaposition de ces charges opposées porte le nom de dipôle électrique. On dit encore que la molécule ou la liaison possède un moment dipolaire. Ce moment est un vecteur dont on sait seulement déterminer expérimentalement le module. Cette mesure donne des renseignements sur la configuration géométrique des molécules et le caractère ionique ou non de leurs liaisons de valence.

L’étude des moments dipolaires est inséparable de celle de la constante diélectrique, ou permittivité, dans des champs de différentes fréquences, qui mettent en évidence des phénomènes d’absorption conditionnant la relaxation diélectrique. Par ailleurs, la polarité des molécules détermine les forces moléculaires à l’état liquide et les grandeurs thermodynamiques qu’elles gouvernent (constantes critiques, chaleur de vaporisation, température d’ébullition, etc.).

1. La polarité des molécules

D’un point de vue formel, le problème général des interactions entre molécules chimiques comporte deux étapes: le calcul du champ électrique produit par une molécule en un point extérieur, puis l’action de ce champ électrique sur une autre molécule. Le traitement rigoureux de chaque question exige la connaissance précise, rarement atteinte, de la distribution des charges électriques dans chaque molécule. On peut, le plus souvent, se contenter d’une solution approchée en caractérisant la molécule par un vecteur, son moment de dipôle électrique.

Cette notion se précise si on considère le système des forces みappliquées à une molécule plongée dans le champ électrique つ, et si on assimile cette molécule à un ensemble de charges ponctuelles q ^j de positions définies par les vecteurs る^j . La résultante générale de ce système de forces, づ = み^j = つ q ^j , est nulle dans le cas d’une molécule électriquement neutre, de sorte que l’action d’ensemble du champ se réduit à un couple caractérisé par le moment résultant:

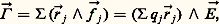ce qui introduit le moment électrique total ゙ = q ^j size=1^るj . L’action du champ つ entraîne une déformation de la molécule que l’on traduit en posant る^j = るj + ぴ^j , où るj se rapporte à la configuration de la molécule en l’absence de champ. Le moment électrique total comporte ainsi deux termes, dont le premier, ゙⁰ = q ^j size=1^る j , définit le moment électrique permanent (ou moment dipolaire, ou dipôle permanent) de la molécule et le second, ゙ⁱ = q ^j size=1^ゎj , représente le moment électrique induit, proportionnel au champ つ.

Le moment permanent ゙⁰ peut être nul pour certaines molécules; lorsqu’il n’en est pas ainsi, on dit qu’il s’agit de molécules polaires. La distinction entre molécules polaires et non polaires intervient pour l’ensemble des propriétés de la matière.

Les molécules polaires sont donc caractérisées par leur dipôle permanent 猪 ⁰, c’est-à-dire par un système de deux charges opposées + q et 漣 q , dont la distance a est de l’ordre de grandeur des dimensions moléculaires. La charge q a une grandeur voisine de la charge élémentaire, de sorte que 猪 ⁰ = qa , exprimé dans l’ancien système d’unités u.e.s., est de l’ordre de 10^-18. En conséquence, l’unité usuelle de moment dipolaire, le debye (D), a été choisie telle que 1 D = 10^-18 u.e.s. = 3,335 64 . 10^-30 coulomb . mètre (unité SI). La décomposition 猪 ⁰ = qa est sans intérêt, sauf pour le calcul théorique à partir de la distribution des charges; le moment 猪 ⁰ est la seule grandeur accessible à l’expérience et intervient par son module, sa direction par rapport à la molécule et son sens, qu’on note habituellement en prenant le pôle positif comme origine: H 漣Cl 轢. Les moments en phase gazeuse sont généralement de l’ordre de quelques debyes (eau, 1,85 D; chloroforme, 1,01 D; acétone, 2,86 D; acide chlorhydrique, 1,08 D).

2. Mise en évidence et mesure du moment permanent

La grandeur physique la plus directement gouvernée par la présence d’un moment moléculaire permanent est la constante diélectrique relative 﨎 ^r, ou permittivité relative, qui définit l’accroissement de la capacité d’un condensateur électrique lorsqu’on remplit de matière l’espace entre les armatures. La relation entre 﨎 ^r et le moment électrique s’établit par l’intermédiaire du moment électrique par unité de volume, ou polarisation électrique は, de la substance. Cette polarisation entraîne (fig. 1) l’augmentation de la densité de charge électrique 靖 des armatures, de manière à conserver le même champ électrique つ qu’en l’absence de matière, qui correspond à la densité 靖 . La relation 靖 漣 P = 靖 ou 靖 = 靖 + P s’écrit, en introduisant l’induction électrique っ:

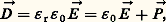où 﨎 ⁰, permittivité du vide, a pour valeur 8,854 2 . 10^-12 F/m dans le système SI et 1/4 神 dans le système u.e.s.

La polarisation électrique P s’interprète comme la somme des contributions moyennes 猪 des molécules, au nombre de N par unité de volume, soit P = N 猪 , d’où la relation générale:

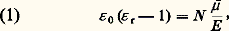et, en u.e.s.:

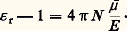Le moment électrique moyen 猪 peut ainsi être obtenu à partir de 﨎 ^r déterminable expérimentalement, et la théorie des diélectriques a pour objet de relier 猪 au moment permanent 猪 ⁰ et au moment induit 猪 ⁱ définis ci-dessus.

3. Principes de la théorie des diélectriques

Cas des gaz

Le problème est simple dans le cas des gaz, les molécules étant suffisamment distantes, en moyenne, pour que leurs interactions puissent être négligées. S’il s’était agi d’une substance non polaire, la seule cause de polarité serait le moment induit, qui est en première approximation proportionnel au champ appliqué つ, soit ゙ = ゙ⁱ = 見 つ. Le coefficient 見 représente la polarisabilité moyenne, ou susceptibilité électrique moyenne, de la molécule. Le qualificatif «moyenne» rappelle le caractère tensoriel et non scalaire de la relation entre les vecteurs ゙ⁱ et つ. Pour une substance non polaire, la relation (1) s’écrit alors:

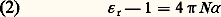dans le système u.e.s., qui demeure le plus utilisé dans les traités spécialisés.

Lorsque la substance est polaire, il faut ajouter la contribution des dipôles permanents. En l’absence de champ électrique extérieur, l’agitation brownienne assure l’orientation au hasard des dipôles, d’où une valeur nulle de leur résultante. Le champ exercé つ tend à conférer une orientation commune à ces dipôles, mais cette action, contrariée par l’agitation thermique, demeure extrêmement faible; l’état de saturation, où tous les dipôles seraient parallèles au champ, est absolument inaccessible par suite des effets d’ionisation et de claquage dus aux champs électriques élevés, contrairement au comportement d’une substance paramagnétique dans un champ magnétique.

Le calcul statistique montre que dans le cas des champs électriques relativement faibles, auquel on est ainsi pratiquement limité, l’effet obtenu par cette orientation des dipôles est équivalent à un accroissement de la polarisabilité, de valeur 見 size=1^猪 = 猪 ⁰²/3kT , qu’on désigne sous le nom de polarisabilité d’orientation (k est la constante de Boltzmann). L’énergie cinétique moyenne par degré de liberté, kT , exprime le rôle de l’agitation thermique à la température thermodynamique T , qui tend à s’opposer à l’action d’orientation du champ. Pour les molécules polaires, la relation (2) est alors remplacée par:

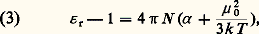en groupant les deux contributions inséparables de 猪 ⁱ et de 猪 ⁰. La mesure de 﨎 ^r ne permet donc pas à elle seule d’accéder à la connaissance du moment permanent.

Une première méthode de mesure consiste à déterminer 﨎 ^r à deux températures différentes au moins, en s’appuyant sur le fait que 見 , qui est une grandeur moléculaire, demeure inchangée. Bien que la mesure de la permittivité d’un gaz soit délicate, ce procédé est utilisé et donne des résultats précis lorsque la substance dont on veut mesurer le moment est suffisamment volatile.

Une seconde méthode permet de connaître 猪 ⁰ à partir de la mesure de 﨎 ^r à une température donnée, en utilisant la propriété des champs de fréquence suffisamment élevée de ne plus orienter les dipôles électriques, par suite de l’inertie moléculaire. Les fréquences minimales pour qu’il en soit ainsi, et qui marquent la limite du domaine de la relaxation diélectrique, appartiennent, pour la plupart des molécules, au domaine des ondes millimétriques. Pour ces champs de haute fréquence, la relation (3) s’écrit, si on laisse de côté la polarisation d’orientation: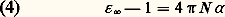

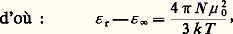en désignant par 﨎 size=1^秊 la valeur de la permittivité pour ces fréquences élevées.

De telles mesures sont délicates; en général, on se contente d’effectuer la mesure dans le domaine plus éloigné des radiations lumineuses, où elle se ramène à une mesure d’indice de réfraction n grâce à la relation de Fresnel 﨎 = n ². Le choix usuel 﨎 size=1^秊 力 n ² permet ainsi de déterminer 見 à partir de la mesure de l’indice de réfraction pour une radiation visible, généralement la raie D du sodium, mais ne peut pas prétendre à une bonne définition, à cause des phénomènes de dispersion qui entraînent la variation de l’indice n avec la longueur d’onde de mesure.

Cas des liquides

Une difficulté essentielle dans le cas des liquides réside dans le fait que le champ effectif 劉 agissant sur une molécule donnée – et qui intervient dans l’évaluation de 猪 – est distinct du champ électrostatique つ qui figure dans la relation (1). Cet important problème du champ effectif, qui apparaît dans de nombreuses théories de la matière condensée, a été abordé en premier lieu par Hendrik Antoon Lorentz. Sa théorie permet de traiter le cas de substances de faible permittivité. C’est celui d’une solution diluée d’un constituant polaire 1, de moment ゙⁰ dans un solvant non polaire 2, et l’on parvient ainsi à la relation dite de Clausius-Mossotti:

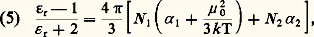où N ¹ et N ² désignent le nombre de molécules de chaque espèce par unité de volume.

L’application de cette relation à la détermination de ゙⁰ se fait généralement en mesurant l’indice de réfraction du mélange, et en faisant l’approximation 﨎 size=1^秊 力 n ², ce qui conduit à la relation:

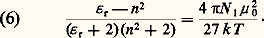Ces relations ne sont pas utilisables lorsque le rapport 﨎 ^r/n ² s’écarte sensiblement de l’unité, comme c’est généralement le cas lorsqu’il s’agit d’une substance polaire à l’état pur ou en solution non diluée dans un solvant non polaire. Une analyse plus détaillée du champ effectif a conduit Lars Onsager à la très importante relation suivante (toujours dans l’approximation 﨎 size=1^秊 力 n ²);

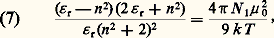Il en résulte notamment que, pour les liquides non polaires, on doit avoir 﨎 ^r = n ², c’est-à-dire que la permittivité relative doit conserver la même valeur depuis la détermination statique jusqu’à celles en haute fréquence, même dans le domaine des radiations visibles. Ce critère de l’absence de moment permanent est bien vérifié; on obtient ainsi, dans le cas du benzène, 﨎 ^r = 2,28 et n ² = 2,26 à 20 ⁰C, alors que ces quantités diffèrent beaucoup lorsqu’il s’agit d’une substance polaire comme l’acétone, pour laquelle 﨎 ^r = 20,70 et n ² = 1,95.

En conclusion, la détermination du moment permanent d’une substance peut être effectuée à partir de mesures de permittivité et d’indice, soit sur le liquide pur, soit sur des solutions étendues dans des solvants non polaires. Cette dernière méthode, qui présente l’avantage d’éviter l’influence perturbatrice des auto-associations éventuelles du composé polaire, est la plus utilisée, et la plupart des valeurs figurant dans les tables sont obtenues par cette voie. Cette méthode exige une détermination précise de la variation relativement faible de la permittivité lorsqu’on passe du solvant pur à la solution, ce qui demande une très bonne qualité de l’appareillage et la régulation de la température de la cellule de mesure. Il existe un certain nombre de réalisations commerciales utilisant des ponts de mesure et connues sous le nom de dipôlemètres.

L’exploitation des mesures en phase liquide, aboutissant aux relations 6 et 7, suppose une certaine isotropie de la molécule, tant du point de vue géométrique qu’optique, conditions souvent mal réalisées dans la pratique. Cela explique les différences entre les valeurs proposées par les tables, suivant la nature du solvant et la température de mesure, les écarts pouvant être de l’ordre de grandeur de 0,1 D. Les corrections proposées pour tenir compte de cet effet de solvant ne peuvent pas encore être considérées comme très sûres.

Les déterminations à partir de la mesure de 﨎 ^r, en phase gazeuse échappent à ces effets, mais sont difficiles à mettre en œuvre. D’où l’intérêt de la méthode fondée sur l’étude du spectre de rotation pure de la molécule par spectrographie micro-ondes à modulation Stark. Il s’agit d’une méthode de résonance, donc très précise, qui exclut toute complication d’interactions moléculaires, du fait des faibles pressions dans la cellule (face=F0019 麗 10 Pa); mais l’exploitation des résultats est très difficile lorsque les molécules n’appartiennent pas au modèle de la toupie symétrique, c’est-à-dire que leur ellipsoïde d’inertie n’est pas de révolution.

4. Moment dipolaire et structure moléculaire

Représentation par moments de liaison

La démarche habituelle en physico-chimie, qui consiste à tenter la représentation d’une grandeur moléculaire quelconque comme somme d’incréments de liaison, aboutit dans le cas du moment dipolaire à introduire des moments de liaison de caractère vectoriel. Leur direction est celle de la liaison et leur sens est donné par la différence d’électronégativité entre les atomes liés, ce qui conduit ainsi à la notation C 漣Cl 轢. La connaissance de ces moments de liaison résulte de l’analyse du moment moléculaire total, seul accessible, ce qui ne va pas sans quelque arbitraire. Il n’y a pas de difficulté pour les carbures saturés, non polaires, ce qui s’interprète aisément comme une conséquence de la disposition tétraédrique des liaisons, et cela quelle que soit la valeur du moment de la liaison C 漣 H, qui n’est pas directement accessible. La présence d’un faible moment chez certains carbures – 0,13 D pour l’isobutane HC(CH³)³ par exemple – s’explique par la déformation de la molécule consécutive à l’encombrement stérique des groupements méthyles.

Ce moment de la liaison C 漣H s’introduit comme une constante inconnue dans la plupart des autres déterminations. C’est ainsi que la substitution d’un atome d’hydrogène par un atome de chlore donne à tous les chlorures d’alcoyle pratiquement le même moment de 2,10 D, qui représente 猪 (C 漣Cl 轢) 漣 猪 (C 漣H 轢), ces deux moments étant supposés arbitrairement de même sens.

L’extension de cette méthode de proche en proche conduit à dresser des tables de moments de liaison qui permettent le calcul approché du moment d’une molécule de géométrie connue. Les écarts à la loi d’addition vectorielle des moments de liaison s’interprètent en général aisément.

C’est ainsi que les moments des composés CH³Cl et CHCl³ sont respectivement 1,87 D et 1,01 D, alors que le calcul à partir des moments de C 漣H et de C 漣Cl devrait conduire à la même valeur. Lors du passage du chlorure de méthyle au chloroforme, le moment 猪 (C 漣H 轢) croît certainement, alors que 猪 (C 漣Cl 轢) diminue, ce qui va bien dans le sens observé; en outre, il faut probablement tenir compte des moments induits portés par les atomes de chlore, fortement polarisables, la contribution relative des deux effets étant malaisée à évaluer.

Un exemple des hypothèses arbitraires introduites dans le calcul des moments de liaison est donné par la détermination de 猪 (C 漣O 轢), à partir du moment de l’éther méthylique (fig. 2). La composition des moments permet d’écrire:

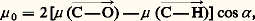en supposant nulle la contribution des doublets électroniques libres de l’atome d’oxygène. Le procédé n’a pas d’inconvénient tant que les moments obtenus sont utilisés dans la comparaison de molécules de structures voisines, mais il leur enlève toute signification physique. Le rôle joué par ces doublets électroniques devient d’ailleurs manifeste quand on veut interpréter la différence entre le moment de l’ammoniac (1,47 D) et celui du trifluorure d’azote (0,23 D), alors qu’il est vraisemblable a priori que le moment 猪 (N 漣F 轢) doit être, en valeur absolue, supérieur à 猪 (N 漣H 轢). Dans le premier cas (fig. 3 a), le moment du doublet libre de l’atome d’azote s’ajoute à celui des liaisons N 漣H, alors qu’il se retranche de la résultante des 猪 (N 漣F 轢) dans le second cas (fig. 3 b).

Malgré ces difficultés, la valeur du moment dipolaire d’une molécule constitue un élément d’information important dans l’étude de sa structure. La valeur nulle du moment du dioxyde de carbone n’est, par exemple, conciliable qu’avec la structure linéaire symétrique OCO. Inversement, la valeur du moment de l’eau oxygénée H²² (2,10 D) exclut toute structure symétrique et confirme la non-planéité de la structure (fig. 4); on peut alors évaluer correctement l’angle des deux plans définis chacun par la liaison O 漣O et l’un des hydroxyles.

Le cas des composés non saturés introduit d’autres contributions à la valeur du moment total. C’est ainsi que la différence significative entre le moment du monochloroéthylène (1,45 D) et celui du chlorure d’éthyle (2,10 D) est attribuable en partie au fait que les orbitales trigonales du carbone confèrent ici aux liaisons C 漣H et C 漣Cl des moments différents de ceux qui interviennent dans le composé saturé; dans ce composé les liaisons avec le carbone sont assurées par des orbitales tétraédriques; il s’y ajoute encore la contribution de la forme mésomère 漣CH² 漣CH = +Cl, dont le moment tend à s’opposer à celui de la forme principale. Les deux effets ne sont pas séparables, ce qui enlève un peu de précision à la notion de moment mésomère qu’on introduit souvent pour rendre compte des écarts à l’additivité des moments de liaison, du fait de la conjugaison.

Le rôle de cet effet peut être mis en évidence par la comparaison des moments des isomères du chloronitrobenzène. Ce moment est la résultante des moments de liaison des deux substituants, connus à partir des dérivés monosubstitués (C⁶H⁵², 3,93 D; C⁶H⁵Cl, 1,58 D), qui s’obtient immédiatement, compte tenu de l’angle des liaisons (60⁰, 120⁰, 180⁰) [fig. 5]. La comparaison des valeurs ainsi calculées et des valeurs déterminées expérimentalement ne permet aucun doute sur l’identification des isomères, l’accord étant toutefois meilleur dans le cas de l’isomère méta, pour lequel les formes mésomères sont indépendantes. Le calcul suppose une hypothèse sur le sens relatif des moments des deux substituants qui sont ici de même sens et se retranchent ainsi dans le dérivé para. Si ce résultat était attendu dans ce cas, il n’en est pas toujours de même, et l’étude du moment des isomères CHXY est un bon moyen de connaître le sens relatif des moments C 漣X et C 漣Y.

Théories moléculaires du moment dipolaire

La connaissance précise de la fonction d’onde multiélectronique d’une molécule permet le calcul du barycentre de ses n électrons par la relation:

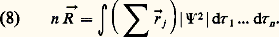Il suffit, d’autre part, de calculer le barycentre des charges positives nucléaires pour obtenir les deux pôles opposés qui définissent le moment permanent de la molécule. De bons résultats sont obtenus, même en utilisant des orbitales L.C.A.O. semi-empiriques, l’accord étant d’ailleurs un test sévère de la valeur de la fonction d’onde utilisée.

La principale difficulté apparaît lorsque l’on tente de décomposer le moment global en composantes telles que les moments de liaison, ce qui est lié au fait que dans une fonction d’onde électronique les électrons ne sont pas individualisés et ne peuvent donc être considérés comme localisés sur une liaison donnée. Cependant, une bonne justification du principe de la décomposition en incréments est fournie par la méthode des loges (due à Raymond Daudel), dans laquelle on considère que certains domaines correspondant en gros aux liaisons et aux doublets libres conservent une charge électronique constante, bien que ce ne soient pas toujours les mêmes électrons qui la constituent. Par contre, la mise en œuvre d’une telle décomposition pose des problèmes délicats et dépend de l’approximation adoptée dans la représentation des fonctions d’onde. La liaison simple est souvent interprétée comme hybride des formes purement covalente et ionique (représentation de Pauling), ce qui se traduit dans le langage des fonctions d’onde, abstraction faite de la normation, par 切 = 切^cov. + 切^ion., avec un taux de caractère ionique ²/(1 + ²). Dans cette représentation, le moment dipolaire de la liaison est attribué à la participation de la forme ionique égale à eR , où R est la distance des deux atomes liés, de sorte que 猪 ⁰/eR constitue une mesure du taux de caractère ionique ci-dessus, qu’on peut confronter à celui qui est déduit de considérations énergétiques ou, ce qui revient au même, à la différence de l’incrément d’électronégativité 﨑 des atomes liés (fig. 6). Cette représentation, très importante parce que simple, suppose plusieurs hypothèses. Tout d’abord, la contribution de la forme purement ionique laisse de côté la perturbation due à la polarisation mutuelle des ions, ce qui est acceptable, la déformation électronique qui s’ensuit pouvant être mise au compte de la participation de la forme covalente. L’hypothèse d’une valeur nulle du moment de la forme purement covalente est plus gênante. Elle a été examinée par Charles Alfred Coulson, qui a montré qu’elle cessait d’être acceptable lorsque les atomes liés étaient de tailles très différentes. Enfin, le calcul se complique et perd beaucoup d’intérêt lorsque l’on veut tenir compte de l’intégrale de recouvrement des deux formes, dont la valeur est d’ailleurs le plus souvent inconnue.

L’approximation ci-dessus est pratiquement limitée au cas des molécules diatomiques et on s’est orienté, pour les molécules polyatomiques, vers le calcul direct des moments de liaison A 漣B à partir d’orbitales monoélectroniques L.C.A.O. de la forme 祥 = 祥^A + 祥^B, où le paramètre tient compte de la différence d’électronégativité des atomes liés (méthode des orbitales de liaison). Le calcul du barycentre électronique fait apparaître les termes:

les orbitales étant supposées réelles. Si on prend l’origine sur le noyau A, la contribution des deux dernières intégrales au moment de liaison dépend de la distance des noyaux, mais non pas la première, si ce n’est, faiblement, par le coefficient de normation de 祥. Cette contribution est nulle si 祥^A est symétrique (orbitale s ou p ), mais non s’il s’agit d’une orbitale hybride. Le dipôle atomique qui représente cette contribution est particulièrement important (2,2 D) pour le carbone dans l’hybridation tétraédrique, et la question est de savoir s’il faut le compter ou non dans l’évaluation du moment de liaison. En fait, dans le calcul du moment total, il y a généralement compensation des moments atomiques portés par les liaisons afférentes à un même atome, sauf évidemment lorsqu’il existe des doublets électroniques libres, dont on est bien obligé de tenir compte lors de la composition des moments de liaison.

5. Utilisation des moments dipolaires

On ne reviendra pas sur les informations fournies par cette grandeur dans l’étude des structures moléculaires. Mentionnons d’autres travaux utilisant cette caractéristique moléculaire.

Tout d’abord, on s’est limité à des molécules de moment bien défini; mais toute déformation, une rotation gênée par exemple, se traduit par une valeur apparente du moment, variable avec la température de mesure. L’analyse est particulièrement simple dans le cas du dichloroéthane, qu’on peut interpréter comme résultant de l’équilibre de deux rotamères (fig. 7), dont l’un possède un moment nul, ce qui permet le calcul du moment moyen apparent à partir de la forme polaire, compte tenu du poids statistique de chaque forme, soit: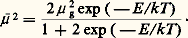

On conçoit ainsi l’importance de cette méthode dans l’étude des molécules déformables, qui permet d’accéder à la différence d’énergie des diverses formes.

Une méthode d’étude des associations en solvants non ionisables peut également se déduire des relations précédentes. La relation de Clausius-Mossotti se généralise sans difficulté au cas de mélanges et permet de mettre en évidence des associations dont le moment est le plus souvent supérieur à celui des constituants. Cette méthode, limitée à des solutions diluées, peut être étendue à des solutions concentrées en généralisant la relation (7) de Onsager au cas d’un mélange de constituants polaires.

Une des associations en phase liquide les plus fréquentes est constituée par la liaison hydrogène, dont le moment important (face=F0019 黎 3 D) peut être interprété par la contribution d’une forme mésomère ionique A 漣H—-B 兩 (A 漣H)^-B⁺. La valeur considérable de ce moment confère une permittivité élevée aux liquides associés tels que l’eau, les alcools ou l’acide cyanhydrique. Sans aucun doute, l’accumulation de telles liaisons dans de nombreux composés d’intérêt biologique doit jouer un grand rôle. Ce domaine est encore peu exploré, et on se contentera de citer l’exemple d’un polymère synthétique, le poly-L- 塚 glutamate de benzoyle. Sa structure en hélice 見 droite (fig. 8) est stabilisée par des liaisons N 漣H—-O 略 C dont les moments concordants déterminent une valeur du moment résultant proportionnelle à la longueur de l’hélice et, de ce fait, particulièrement élevée.

6. Développements récents

Tout d’abord, le progrès dans le calcul ab initio des structures moléculaires permet de disposer de meilleures fonctions d’onde et d’atteindre avec une précision satisfaisante les polarisabilités et le moment permanent d’une molécule.

Ensuite, la considération exclusive des effets dipolaires apparaît souvent comme insuffisante et l’extension à l’étude des moments électriques multipolaires, que l’on sait maintenant calculer et mesurer, apparaît nécessaire.

Enfin, la théorie classique des molécules polaires en solution utilisait l’approximation dite du modèle de cavité, consistant à assimiler l’entourage d’une molécule à un continuum. Des progrès significatifs ont été accomplis en vue de dépasser cette approximation; la difficulté tenant au caractère «coopératif» des interactions moléculaires a pu être surmontée au moyen de méthodes mathématiques élaborées faisant appel souvent à l’emploi de graphes. L’étude des molécules polaires en phase condensée devient ainsi intégrée dans la théorie générale de l’état liquide.

Encyclopédie Universelle. 2012.